力扣-11. 盛最多水的容器（Container With Most Water）

最后编辑于2025-06-10

11. 盛最多水的容器（Container With Most Water）

Medium

给定一个整数数组 height 长度为 n，第 i 条竖线的坐标为 (i, 0) 和 (i, height[i])。

找出两条线，使得它们与 x 轴一起形成的容器可以装下最多的水，返回容器可以存储的最大水量。注意容器不能倾斜。

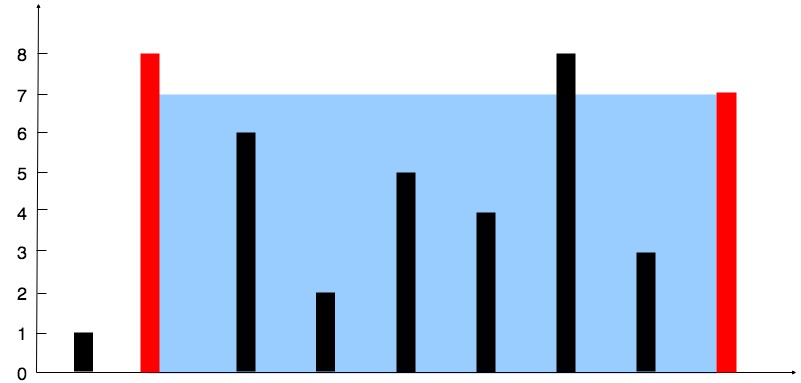
示例 1：


输入： height = [1,8,6,2,5,4,8,3,7]
输出： 49

解释： 选取第 1（高度 8）和第 8（高度 7）两条线，面积为 min(8,7) * (8-1) = 7 * 7 = 49。

示例 2：

输入： height = [1,1]
输出： 1

约束：

  • n == height.length
  • 2 <= n <= 10^5
  • 0 <= height[i] <= 10^4

解题思路（双指针 + 贪心）

观察发现，容器面积由两部分决定：宽度 j - i 与高度 min(height[i], height[j])。暴力枚举所有对需要 O(n^2)，输入规模较大时不可行。

使用双指针从数组两端向中间逼近：初始 i = 0, j = n-1，每步计算面积并更新结果。然后移动指向较短高度的指针（若 height[i] < height[j]，则 ++i，否则 --j）。理由是：移动较高的一侧不会在宽度缩小的同时带来更高的高度上界，无法产生更大面积，因此应移动较短的一侧以期望找到更高的边界从而弥补宽度减少造成的损失——这是个贪心策略。该方法时间复杂度 O(n)，空间复杂度 O(1)。

方法一：双指针（简单版）

1
2
3
4
5
6
7
8
9
10
11
12
class Solution {
public:
    int maxArea(vector<int>& height) {
        int res = 0, i = 0, j = height.size() - 1;
        while (i < j) {
            res = max(res, min(height[i], height[j]) * (j - i));
            if (height[i] < height[j]) ++i;
            else --j;
        }
        return res;
    }
};
  • 时间复杂度： O(n)
  • 空间复杂度： O(1)

方法二：双指针（跳过相等高度的优化）

在遇到某一侧高度等于当前较小高度时，可以一次性跳过所有相等的高度，减少重复计算，但仍然保持 O(n) 复杂度。示例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
class Solution {
public:
    int maxArea(vector<int>& height) {
        int res = 0, i = 0, j = height.size() - 1;
        while (i < j) {
            int h = min(height[i], height[j]);
            res = max(res, h * (j - i));
            while (i < j && height[i] == h) ++i;
            while (i < j && height[j] == h) --j;
        }
        return res;
    }
};
  • 时间复杂度： O(n)
  • 空间复杂度： O(1)

作者想说的话：
本题核心是双指针配合贪心策略：在宽度不断减小的过程中，只移动能带来更高上界的一侧（即移动较低的边），从而在一次线性扫描内找到最优解。